Principles of Hindu Reckoning

Principles of Hindu Reckoning (Kitab fi usul hisab al-hind) is a mathematics book written by 10th–11th-century Persian mathematician Kushyar ibn Labban. It is the second-oldest book extant in Arabic about Hindu arithmetic using Hindu numerals( ० ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹), preceded by Kibab al-Fusul fi al-Hisub al-Hindi by Abul al-Hassan Ahmad ibn Ibrahim al-Uglidis, written in 952. Although Al-Khwarzimi also wrote a book about Hindu arithmetics in 825, he did not use Hindu numerals, and the Arabic original was lost, only a 12th century translation is extant. Kushyar ibn Labban did not mention the Indian sources for Hindu Reckoning, and there is no earlier Indian book extant which covers the same topics as discussed in this book. Principles of Hindu Reckoning becomes one of the foreign sources for Hindu Reckoning in the 10th–11th century in India.

Contents

Indian dust board

Hindu arithmetic was conducted on a dust board similar to the Chinese counting board. A dust board is a flat surface with a layer of sand and lined with grids. Very much like the Chinese count rod numerals, a blank on a sand board grid stood for zero, and zero sign was not necessary.[1]Shifting of digits involves erasing and rewriting, unlike counting board.

Content

There is only one Arabic copy extant, now kept in the Aya Sophya Library in Istanbul. There is also a Hebrew translation with commentary, kept in the Bodleian Library of Oxford University. In 1965 University of Wisconsin Press published an English edition of this book translated by Martin Levey and Marvin Petruck, based on both the Arabic and Hebrew editions. This English translation included 31 plates of facsimile of original Arabic text.[2]

Principles of Hindu Reckoning consists of two parts dealing with arithmetics in two numerals system in India at his time.

The similarity between decimal Hindu algorithm with Chinese algorithm in Mathematical Classic of Sun Zi are striking,[3] except the operation halving, as there was no hybrid decimal/sexagesimal calculation in China.

Decimal arithmetics

Addition

Kushyar ibn Labban described in detail the addition of two numbers.

The Hindu addition is identical to rod numeral addition in Mathematical Classic of Sun Zi[4]

operation Rod calculus Hindu rekoning
Layout Arrange two numbers in two rows Arrange two numbers in two rows
order of calculation from left to right from left to right
result placed on top row Placed on top row
remove lower row remove digit by digit from left to right digit not removed

There was a minor difference in the treatment of second row, in Hindu reckoning, the second row digits drawn on sand board remained in place from beginning to end, while in rod calculus, rods from lower rows were physically removed and add to upper row, digit by digit.

Subtraction

In the 3rd section of his book, Kushyar ibn Labban provided step by step algorithm for subtraction of 839 from 5625. Second row digits remained in place at all time. In rod calculus, digit from second row was removed digit by digit in calculation, leaving only the result in one row.

Multiplcation

Kushyar ibn Labban multiplication is a variation of Sun Zi mulitiplication.

operation Sun Zi Hindu
multiplicant placed at upper row, placed at upper row,
multiplier third row 2nd row below multiplicant
alignment last digit of multiplier with first digit of multiplcant last digit of multiplier with first digit of multiplcant
multiplyier padding rod numeral blanks rod numeral style blanks, not Hindu numeral 0
order of calculation from left to right from left to right
product placed at center row merged with multiplicant
shifiting of multiplier one position to the right one position to the right

Division

Professor Lam Lay Yong discovered that the Hindu division method describe by Kushyar ibn Labban is totally identical to rod calculus division in 5th centuryMathematical Classic of Sun Zi[5]

operation Sun Zi division Hindu division
dividend on middle row, on middle row,
divisor divisor at bottom row divisor at bottom row
Quotient placed at top row placed at top row
divisor padding rod numeral blanks rod numeral style blanks, not Hindu numeral 0
order of calculation from left to right from left to right
Shifting divisor one position to the right one position to the right
Remainder numerator on middle row,denominator at bottom numerator on middle row,denominator at bottom

Besides the totally identical format, procedure and remainder fraction, one tell tell sign which discloses the origin of this division algorithm is in the missing 0 after 243, which in true Hindu numeral should be written as 2430, not 243blank; blank space is a feature of rod numerals (and abacus).

Divide by 2

Divide by 2 or "halving" in Hindu reckoning was treated with a hybrid of decimal and sexagesimal numerals: It was calculated not from left to right as decimal arithmetics, but from right to left: After halving the first digit 5 to get 21⁄2, replace the 5 with 2, and write 30 under it:

5622
30

Final result:

2812
30

Extraction of square root

Kushyar ibn Labban described the algorithm for extraction of square root with example of

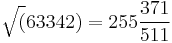
\sqrt(63342)=255\frac{371}{511}

Kushyar ibn Labban square root extraction algorithm is basically the same as Sun Zi algorithm

operation Sun Zi square root ibn Labban sqrt
dividend on middle row, on middle row,
divisor divisor at bottom row divisor at bottom row
Quotient placed at top row placed at top row
divisor padding rod numeral blanks rod numeral style blanks, not Hindu numeral 0
order of calculation from left to right from left to right
divisor doubling multiplied by 2 multiplied by 2
Shifting divisor one position to the right one position to the right
Shifting quotient Positioned at beginning, no subsequent shift one position to the right
Remainder numerator on middle row,denominator at bottom numerator on middle row,denominator at bottom
final denominator no change add 1

The approximation of non perfect square root using Sun Zi algorithm yields result slightly higher than the true value in decimal part, the square root approximation of Labban gave slightly lower value, the integer part are the same.

Sexagesimal arithmetics

Multiplication

The Hindu sexagesimal multiplication format was completely different from Hindu decimal arithmetics. Kushyar ibn Labban's example of 25 degree 42 minutes multiplied by 18 degrees 36 minutes was written vertically as

18| |25
36| |42

with a blank space in between[6]

Influence

Kushyar ibn Labban's Principles of Hindu Reckoning exerted strong influence on later Arabic algorists. His student al-Nasawi followed his teacher's method. Thirteen century algorist Jordanus nemorarius's work was influenced by al-Nasawi. As late as 16th century, ibn Labban's name was still mentioned[7]

Reference

  1. ^ George Ifrah, The Univeral History of Numbers, p554
  2. ^ Martin Levey and Marvin Petruck tr, Kushyar Ibn Labban, Principles of Hindu Reckoning, The University of Wisconsin Press, 1965. Library of Congress Catalog 65-11206
  3. ^ Lam Lay Yong, Ang Tian Se, Fleeting Footsteps, p52
  4. ^ Lam Lay Yong, Ang Tian Se, Fleeting Footstep, p 47 World Scientific
  5. ^ Lam Lay Yong, Ang Tian Se, Fleeting Footstep, p43, World Scientific
  6. ^ Kushyar ibn Labban, Principles of Hindu Reckoning, p80, Wisconsin
  7. ^ Note by Martin Levey and Marvin Petruck to Principles of Hindu Reckoning pp 40–42

External links